Collateral Contagion: Modeling Cascading Slashing Across Restaked Networks

Abstract

This research in collaboration with TokenSight investigates how slashing events in restaked ecosystems can propagate across networks due to shared validator sets, shared LRT portfolios, and overlapping slashing conditions. It introduces a framework for quantifying slashing overlap risk and modeling the amplification and conditional propagation of slashing across networks. The analysis formalizes how correlated validator faults, misaligned delegation strategies, and supermodular attacker incentives can trigger cascading penalties that extend beyond the original fault domain. It also considers how collateral health and LRT portfolio composition influences validator overlap and amplifies cross-network slashing exposure. The framework aims to guide more resilient network design, operator diversification, and risk-aware delegation strategies in restaking-based networks.

The Problem of Cascaded Slashing

Restaking reuses operator stake across multiple networks, improving capital efficiency but also entangling risk. When LRTs or operators serve overlapping networks, a single slashing event can propagate beyond its origin through “contagious” collateral, shared infrastructure, or slashing semantics.

Some cascades remain localized, contained within slash-isolated vaults or delegation boundaries. Others become correlated, spreading systemically through covariant validator sets, portfolios, or dependencies. Furthermore, as stake reuse deepens, so does the covariance potential across participants, raising the probability that a localized fault escalates into a system-wide cascade.

Cascading Modes

Restaking architectures vary in how they contain or propagate slashing risk. Inspired by the modularity of the Rainbow Staking concept, designs can be broadly classified by their fault containment properties: whether slashing propagates locally or systemically.

Localized Slashing

In slash-isolated models, each vault is explicitly partitioned to be slashable by individual networks. As a result, faults remain bounded, such that a validator slashed on one network does not automatically trigger slashes to covariant networks and operators.

Yet, even under localized cascades, second-order effects can emerge:

Collateral contagion: Slashed LRTs used as collateral in lending markets can cause mass liquidations through a decline in NAV, especially in high-LTV or thin-liquidity environments;
Multi-network operator overlap: A single operator slashed across multiple networks simultaneously (e.g. through a downtime incident) triggers multi-network stake drawdown;
Shared infrastructure faults: A shared infrastructure failure or corruption in common RPC endpoints, signing keys, or oracle dependencies can lead to simultaneous localized slashes.

Correlated Slashing

Correlated slashing refers to scenarios where a single validator fault propagates across multiple networks and portfolios due to interdependent stake reuse. Unlike localized slashing, where shared infrastructure may lead to concurrent but contained penalties, correlated slashing arises from a lack of stake isolation, enabling systemic propagation.

At the core is covariance across participants: when networks, validators, or LRTs share validator sets, slashing semantics, infrastructure, or collateral sources, one fault can cascade through all dependent systems. In these architectures, the entire Operator–Network vault is slashable (not just a dedicated portion), removing containment boundaries and heightening contagion risk.

Covariant propagation channels include:

Network A slashed → shared across LRTs X/Z and Operators T/U
LRTs X/Z and Operators T/U service Networks B and C
Slash propagates into Networks B/C, compounding system-wide cascading

The deeper the interdependence, the higher and more durable the slashing severity —extending further into the same second-order effects observed in localized slashing, such as collateral contagion in DeFi, multi-network operator drawdown, and shared infrastructure faults. Each participant’s exposure depends on portfolio overlap, validator reuse, and the strength of emergency containment mechanisms.

Correlated slashing can be further bifurcated into supermodular and submodular attack regimes. In supermodular cases, the attacker’s payoff increases with each additional affected network, as similar infrastructure and slashing conditions or shared validator sets and collateral sources reduce the cost and complexity of executing multi-network attacks. In submodular regimes, the marginal gain from attacking multiple networks decreases as containment strategies enforce differentiation across slashing logic, infrastructure, and stake. Designing for submodularity is essential to suppress attacker incentives and contain systemic fragility.

Restaking Equilibrium

To help assess the nature of a potential slashing event, we introduce a restaking ratio, which measures how much active stake is reused across networks relative to the underlying vault or restaking protocol TVL.

If network A sources 100% of TVL, network B 50%, and network C 70%, the total stake sourced equals 220%, meaning each unit of collateral is reused 2.2 times across the network portfolio.

Higher restaking ratios improve capital efficiency but increase exposure to correlated slashing. Vaults/protocols exceeding a balanced range (e.g., ratio = 2.5–3.5) are penalized with lower restaking scores, reflecting elevated systemic risk.

Effective curation depends on evaluating three dimensions: network risk profiles, collateral quality, and target stake sizing. These metrics help networks determine how much TVL to source, preventing overcommitment that exceeds restaking ratio thresholds and introducing unnecessary systemic risk.

To carefully evaluate each metric refer to:

Restaking Network Risk Evaluation: Developing a Fundamental Approach for network risk profiling;
LRT Slashing Risk’s “Restaked Collateral Quality” ****metric for collateral health evaluation;
Modeling Target Stake Requirements for assessing appropriate target stakes per network.

Modelling Cascades

To quantify how slashing exposure escalates under shared conditions, let’s define the amplified risk function:

Where:

NetworkA is the baseline risk profile score for Network A;
e^S*Λt is an exponential expression using the Nepper coefficient e, which models how baseline risk scales under compounding and continuous exposure:
- S represents the sensitivity coefficient, capturing exposure to covariance, collateral quality, and operator risk;→ Lower values suggest localized containment and reduced correlation risk; higher values indicate systemic fragility from greater overlapping exposure
- Λt designates the temporal propagation amplifier;→ Lower values indicate rapid containment, as in localized cascades; higher values reflect prolonged propagation typical in correlated cascades
R'NetworkA is the amplified risk score result, which reflects correlated propagation effects for Network A.

The expression showcases how slashing risk escalates with overlapping exposure and time-sensitive propagation. Jumping to some practical examples:

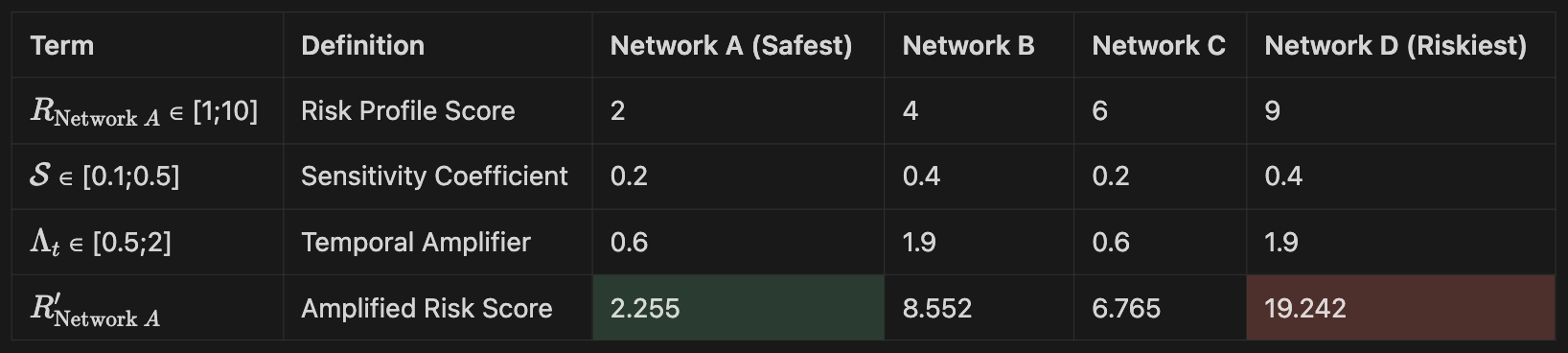
Network A is the safest and Network D the riskiest, both in isolation and in correlation-adjusted terms. Network B shows how moderate baseline risk, when paired with high sensitivity and temporal amplification, can produce a higher systemic risk than a higher baseline score with better containment. Despite scoring lower than Network C in baseline terms (4 vs. 6), Network B’s amplified risk (8.552) exceeds that of Network C (6.765) due to stronger covariance and propagation coefficients. This highlights that baseline risk alone is insufficient and true risk is shaped by how correlated, sensitive, and time-exposed a network is.

Networks A and C exhibit profiles typical of localized slashing, where contagion is limited. Networks B and C, by contrast, reflect contexts of correlated slashing, where covariance amplifies slashing impact.

Let’s now define conditional risk propagation as:

The expression captures the expected slashing impact on Network B given the covariant Network A has been slashed.

This formula captures second-order propagation, where correlations emerge from LRT and validators portfolios overlap, or entangled slashing conditions.

Curators and risk managers must minimize these correlations across portfolios to reduce the likelihood of conditional propagation. Achieving a low propagation requires proactive containment design, including: